https://www.acmicpc.net/problem/1010
지능과 센스가 있으면 쉽게 풀 수 있는 문제. 그러나 난 둘다 없다 ㅎ.
다이나믹 프로그래밍 태그에서 들어간 문제이기 때문에 DP임은 알고 있었다. 이 문제에서 DP를 사용하는 방식은 두가지 가 있는데, 하나는 순수 DP, 하나는 조합론을 사용하는 방법이다.
1. 조합론
이 문제는 2 -> 4 문제로 보이지만, 우측에서 좌측으로 보낸다고 생각하면 언제나 꼬이지 않고 선을 연결할 수 있는 방법이 있다. 그러므로 문제는 갑자기 M combination N 을 구하는 문제로 바뀌어버린다. 그대로 주어진 조합을 구해도 괜찮지만 알다시피 조합은 엄청난 시간복잡도를 자랑하기 때문에 사용하기 어렵다. 이 문제에선 가능하지만 말이다.
그렇다면 조합의 성질을 이용하자.
nCr = n - 1 C r - 1 + n - 1 C r
이것은 마치
dp[n][r] = dp[n - 1][r - 1] + dp[n - 1][r] 과 같다.
2. dp를 사용하는 방법
2에서 3개를 선택하는 것을 가정해보자.
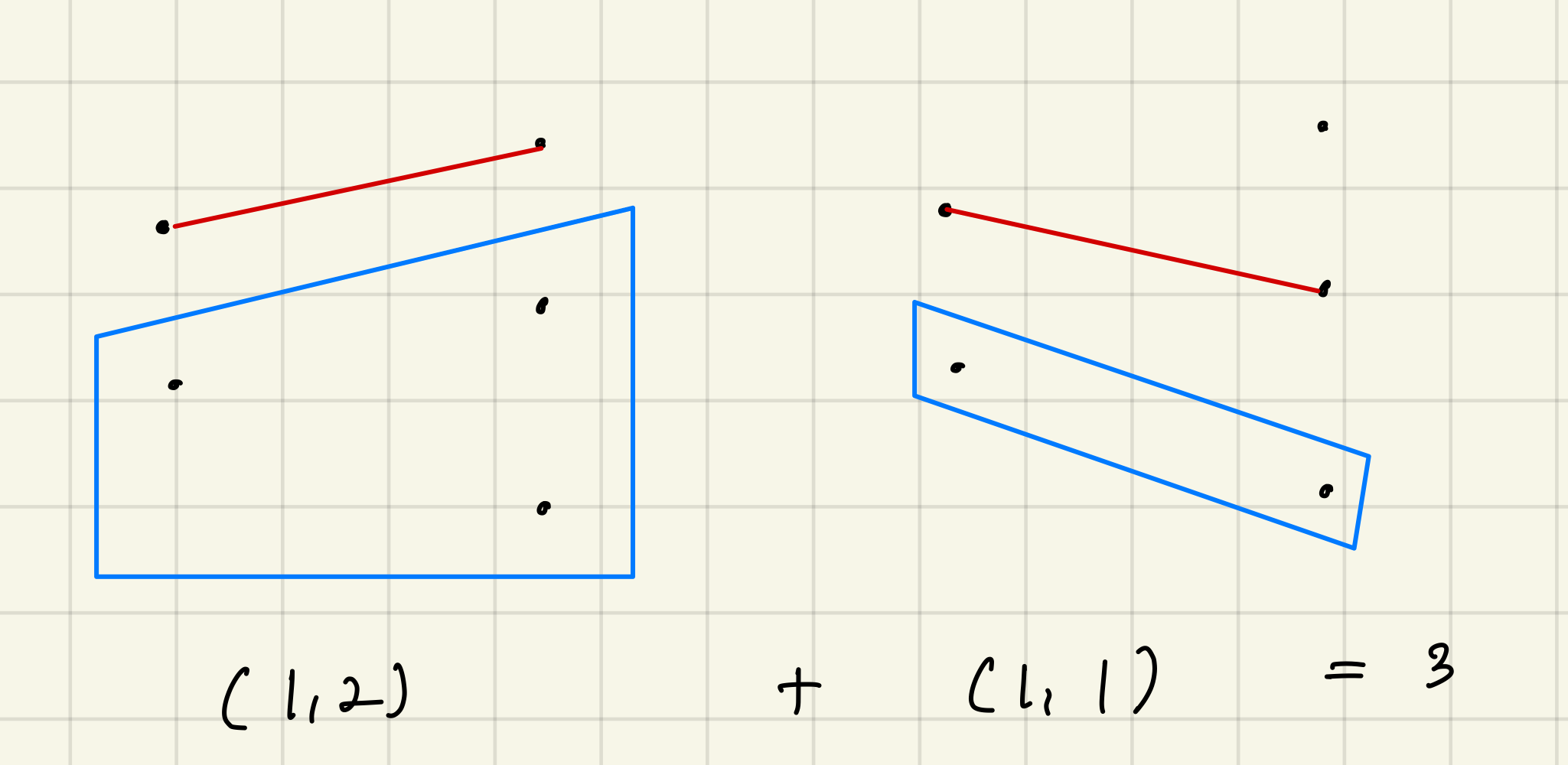
빨간색 선들을 기준선으로 볼 때 뭔가 점화식이 보이는 것 같다. 작은 것들을 사용하여 큰것을 해결하는 정석적인 DP인 Bottom Up 이 보인다. 하지만 하나만 더 해보자. 이번엔 2 -> 4 를 가정하자. 이 점화식이 맞다면 (2, 4) = (1, 1) + (1, 2) + (1, 3) 이 되어야할 것이다.
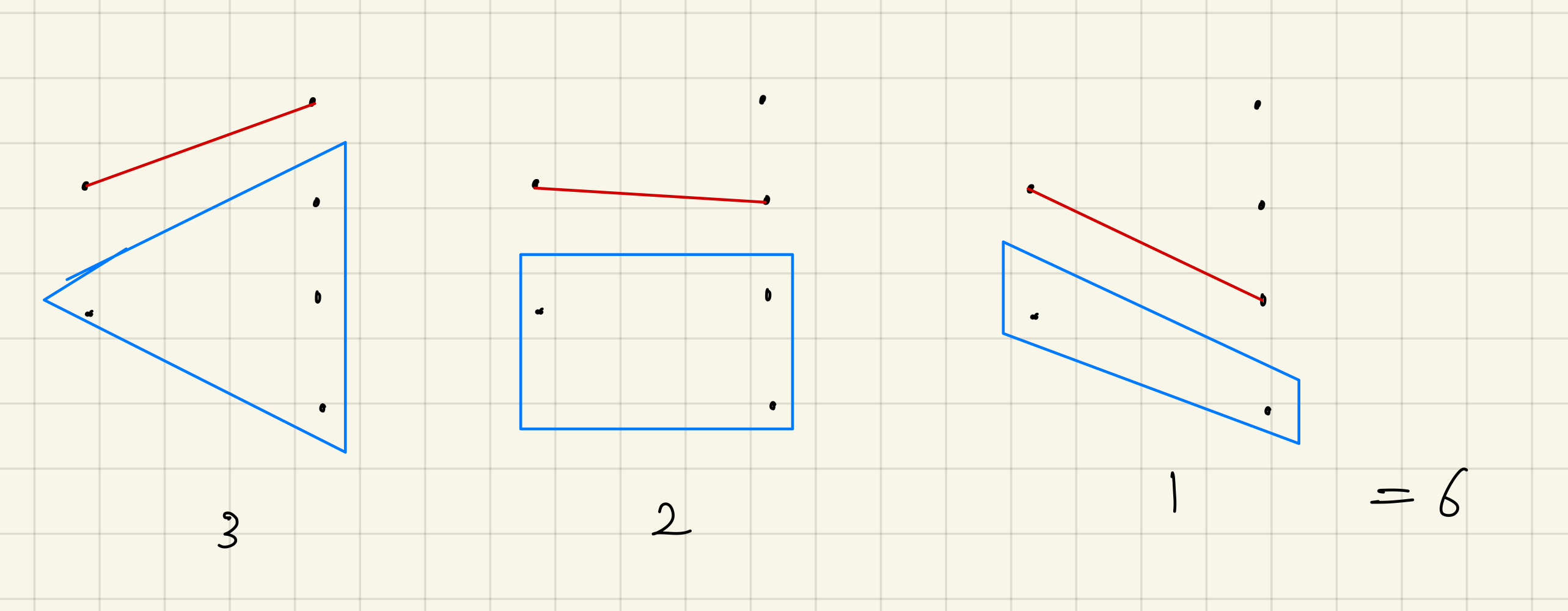

이제 이것을 코드로 바꾸고 dp를 구성한 다음 답을 출력하면 끝이다.
1. 점화식 코드
#include <iostream>
#define ll long long
using namespace std;
int main(){
int T; cin >> T;
ll dp[31][31] = {0,};
for(int i = 1; i < 31; i++){
dp[1][i] = i;
}
for(int i = 2; i < 31; i++){
for(int j = i; j < 31; j++){
for(int x = i - 1; x <= j - 1; x++){
dp[i][j] += dp[i - 1][x];
}
}
}
for(int t = 0; t < T; t++){
int N, M; cin >> N >> M;
cout << dp[N][M] << '\n';
}
}
2. 조합론 코드
#include <iostream>
#define ll long long
using namespace std;
int main(){
int T; cin >> T;
ll dp[31][31] = {0,};
for(int i = 1; i < 31; i++){
dp[i][i] = 1;
dp[i][1] = i;
}
for(int i = 2; i < 31; i++){
for(int j = 2; j < 31; j++){
if(i > j)
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
}
}
for(int t = 0; t < T; t++){
int N, M; cin >> N >> M;
cout << dp[M][N] << '\n';
}
}

'PS > 백준 문제 풀이' 카테고리의 다른 글
| 백준 9328번 - 열쇠(C++) (1) | 2024.06.05 |
|---|---|
| 백준 3015번 - 오아시스 재결합(C++) (0) | 2024.06.05 |
| 백준 1700번 - 멀티탭 스케줄링 (0) | 2024.06.03 |
| 백준 17472번 - 다리 만들기 2 (C++) (0) | 2024.06.02 |
| 백준 17143번 - 낚시왕(C++) (0) | 2024.06.01 |



