728x90
MST는 최소 스패닝 트리의 줄임말로 어떤 그래프가 있을 때 모든 노드를 포함하여 사이클이 생기지 않는 트리를 뜻한다. 한붓그리기를 생각하면 편하다.
크루스칼 알고리즘은 Greedy 알고리즘의 일종이다. 간선을 선택할 때 가장 비용이 적은 간선을 선택하면서 사이클이 생기면 넘어가는 식으로 진행된다.
그렇기 때문에 크루스칼 알고리즘은 모든 간선의 정보가 정렬되어 있어야 사용할 수 있고 모든 간선을 한번씩 검사하기 때문에
시간 복잡도 = 모든 간선의 수 + 정렬 시간
이 소요된다. 사이클을 검사해야하기 때문에 필연적으로 유니온 파인드 알고리즘도 필요하다. 나름 여러 알고리즘이 합쳐진 고급 알고리즘이라 할 수 있다.
정리해보면
1. 간선의 정보들을 모두 정렬한다. 간선의 비용이 적은 순서대로
2. 선택한 간선들을 유니온 파인드로 묶는다.
3. 만약 간선을 선택했을 때 사이클이 발생한다면 간선을 선택하지 않는다.
모든 간선을 검사할 때 까지 반복한다.
난 여기서

이러한 그래프를 구성했고 이 그래프의 최소 스패닝 트리는 1 -> 2 -> 3 -> 4 -> 5 의간선을 선택하는 것이고 총 비용은 5가 들 것이다. 이것을 크루스칼 알고리즘 사용했을 때 결과를 보자
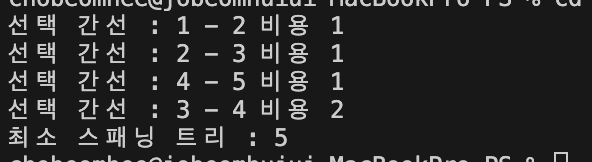
크루스칼 알고리즘의 정의 처럼 작은 비용부터 선택하였다. 전체 코드는 다음과 같다.
#include<iostream>
#include<algorithm>
using namespace std;
struct Node{
int start;
int end;
int cost;
};
int par[10];
bool comp(const Node &a, const Node &b){
if(a.cost == b.cost) return a.start < b.start;
else return a.cost < b.cost;
}
int find(int x){
if(par[x] == x) return x;
else return par[x] = find(par[x]);
}
void Union(int x, int y){
x = find(x);
y = find(y);
if(x < y) par[y] = par[x];
else par[x] = par[y];
}
int main(){
vector<Node> graph;
for(int i = 1; i <= 5; i++) par[i] = i;
graph.push_back({1, 2, 1});
graph.push_back({2, 3, 1});
graph.push_back({3, 4, 2});
graph.push_back({4, 5, 1});
graph.push_back({2, 4, 10});
graph.push_back({2, 5, 12});
sort(graph.begin(), graph.end(), comp);
int MST = 0;
int cnt = 0;
for(auto g : graph){
if(par[g.start] == par[g.end]) continue; // 간선을 선택하면 사이클
cout << "선택 간선 : " << g.start << " - " << g.end << " 비용 " << g.cost << endl;
MST += g.cost;
Union(g.start, g.end);
cnt++;
if(cnt == 4) break;
}
cout << "최소 스패닝 트리 : " << MST << '\n';
}'CS > 자료구조,알고리즘' 카테고리의 다른 글
| 배낭문제에서 넣은 것을 저장하는 아이디어 (0) | 2024.06.29 |
|---|---|
| 누적합 알고리즘(1차원, 2차원 누적합) (0) | 2024.06.22 |
| Dynamic Programming - Top Down, Bottom Up (1) | 2024.06.02 |
| 알고리즘 - 에라토스테네스의 체(C++) (0) | 2024.04.22 |
| unordered_map을 이용한 노드 개수 최적화 (0) | 2024.02.07 |
