https://www.acmicpc.net/problem/2250
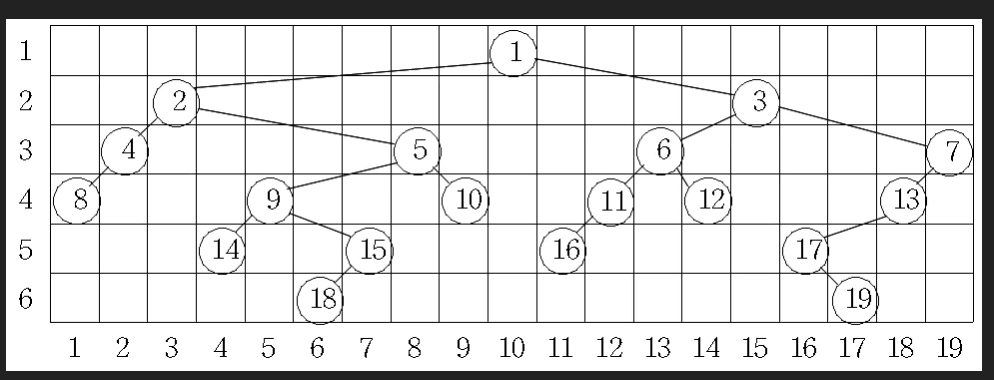
문제는 이해했을 것이고 어떻게 풀어야할까
먼저 이 문제는 root가 정해져있지 않다. 부모가 없으면 그게 루트이고 들어오는 순서들도 루트부터 레벨순으로 들어오지 않음을 유의하자.
이 문제는 한번 N번 노드가 자리를 잡게 한 후 계속 갱신시켜가면 O(2^N) 이상의 시간이 걸린다. 예를 들어 처음에 root를 1번에 자리시킨다고 하자. 그리고 2번, 3번이 들어올 때 마다 자리를 옮긴다면 마지막 18, 19가 들어올 때도 최적의 자리를 위해 모든 노드를 갱신해야할 뿐더러 그것이 최적의 자리인지도 확실하지 않다.
문제의 조건을 보면 각 노드의 컬럼 사이는 비어있지 않다. 그러므로 문제를 최적의 자리를 찾는다에서 반드시 비워둬야할 자리가 몇개인가? 로 생각을 전환해보자.
1번 루트 노드의 경우, left 쪽 트리가 어떻게 구성될지는 모르겠지만 아무튼 9개의 컬럼이 필요하므로 9개의 자리를 비워둬야한다.
2번 노드의 경우도 2자리를 비워둬야한다.
그러므로
col = leftCnt
라는 우선 단순한 추론이 완성되었다. 그러나 5의 경우는?
본인의 왼쪽 노드 후 4개 이외에도 2, 4, 8의 자리를 비워둬야한다. 즉, 자신의 부모의 왼쪽 노드수 + 자신의 왼쪽 노드 수 + 1
col = leftCnt[부모] + leftCnt[본인] + 1
아하.. 그리고 이것은 3번 노드도 마찬가지로 2번과 달리 1번의 왼쪽 노드수를 가지고 가야한다.
그래서 다음과 같은 재귀 로직을 생각할 수 있다.
1. 지금 노드의 위치 = 부모의 왼쪽 노드 수 + 내 왼쪽 노드 수
2. 왼쪽 노드로 이동 -> 부모의 왼쪽 노드 수만 파라미터로 넘기고 내 왼쪽 노드 수는 더하지 않음
3. 오른쪽 노드로 이동 -> 부모의 왼쪽 노드 수 + 내 왼쪽 노드 수 까지 더함
이 핵심 로직과 더불어 트리를 루트에서 전위 순회하며 각 노드의 left와 right를 저장해두고 위의 로직을 진행하면 문제를 풀 수 있다. 약간 DP도 섞여있는 좋은 문제라고 생각한다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct node
{
int level = 1;
int perants = 0;
int left = -1;
int right = -1;
};
int N;
int leftCnt[10001];
int rightCnt[10001];
node tree[10001];
vector<vector<int>> vec(10000 + 1);
int setLeftRightCnt(int n, int lv){
tree[n].level = lv;
if(tree[n].left != -1) {
leftCnt[n] = 1 + setLeftRightCnt(tree[n].left, lv + 1);
}
if(tree[n].right != -1){
rightCnt[n] = 1 + setLeftRightCnt(tree[n].right, lv + 1);
}
return leftCnt[n] + rightCnt[n];
}
void setColPoint(int n, int leftThings){
vec[tree[n].level].push_back(leftThings + leftCnt[n] + 1);
//cout << n << "레벨 :: " << tree[n].level << ' ' << leftThings + leftCnt[n] + 1 << endl;
if(tree[n].left != -1){
setColPoint(tree[n].left, leftThings);
}
if(tree[n].right != -1){
setColPoint(tree[n].right, leftThings + leftCnt[n] + 1);
}
}
int main(){
cin >> N;
for(int i = 0; i < N; i++){
int p, l, r;
cin >> p >> l >> r;
if(l != -1) {
tree[l].perants = p;
}
if (r != -1){
tree[r].perants = p;
}
tree[p].left = l;
tree[p].right = r;
}
int root = 0;
for(int i = 1; i <= N; i++){
if(tree[i].perants == 0) root = i;
}
setLeftRightCnt(root, 1);
setColPoint(root, 0);
int ans = 1;
int lv = 1;
for(int i = 1; i < vec.size(); i++){
vector<int> v = vec[i];
sort(v.begin(), v.end());
if(v.size() > 1){
if(ans < v[v.size() - 1] - v[0] + 1){
ans = v[v.size() - 1] - v[0] + 1;
lv = i;
}
// cout << ans << endl;
}
}
cout << lv << ' ' << ans << '\n';
}

'PS > 백준 문제 풀이' 카테고리의 다른 글
| [백준 1033번] 칵테일 (C++) (0) | 2025.03.31 |
|---|---|
| [백준 2138번] 전구와 스위치(C++) (0) | 2025.03.22 |
| [백준 15824번] 얘 봄에는 캡사이신이 맛있단다 (0) | 2025.03.11 |
| [백준 2515번] 전시장 (C++) (0) | 2025.03.09 |
| [백준 1633번] 최고의 팀 만들기 (C++) (0) | 2025.03.03 |



