LCA: Lowest Common Ancestor
트리의 노드들 중 공통 조상을 찾는 알고리즘이다. DFS, BFS를 통해 한 노드에서 시작해 모든 간선을 확인해볼수도 있겠지만 이 방법을 사용하면 더 빠르게 찾아낼 수 있다.
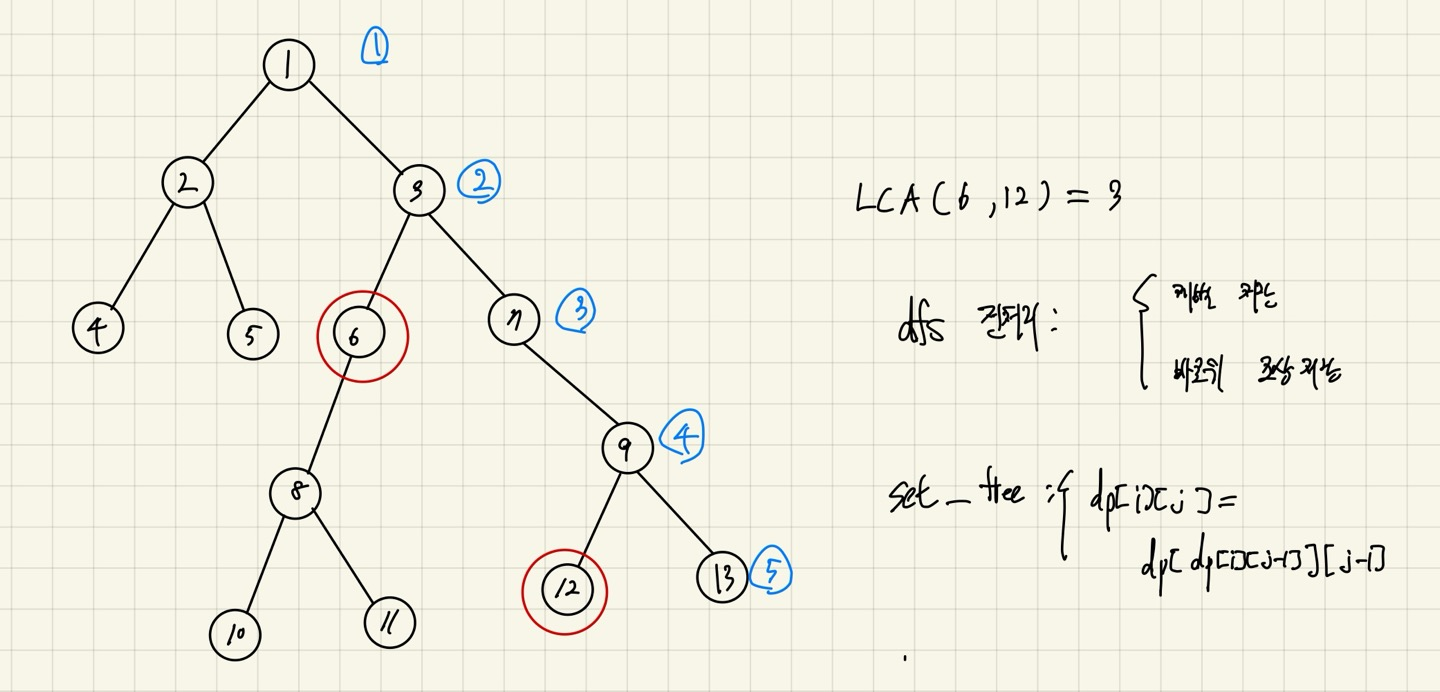
위의 상황에서 12번노드와 6번노드의 최소 공통 조상을 찾아보자. 최소 공통 조상은 누가봐도 3이다. 그렇다면 알고리즘으로 어떻게 풀어낼 수 있을까?
- 레벨을 맞춘다.
LCA에서 중요한 것은 레벨을 맞춰야한다.
즉 LCA(6, 12) = LCA(6, 7) 과 같다.
이처럼 레벨(깊이)를 맞춰준 후 동시에 하나씩 조상을 탐색하는 것이 LCA이다.
DFS 전처리
LCA를 위해서는 각 노드가 조상의 정보와 레벨의 정보를 가지고 있어야한다. 이를 위해 dfs 전처리가 필요하다. 만들어진 노드에서 루트에서 시작해서 각 노드에 조상의 대한 정보와 레벨을 저장해둬야한다.
void dfs(int here,int depth) {
visited[here] = true;
d[here] = depth;
for (int there : vt[here]) {
if (visited[there])
continue;
par[there][0] = here;
dfs(there, depth + 1);
}
}
void f() {
for (int j = 1; j < 21; j++) {
for (int i = 1; i <= n; i++) {
par[i][j] = par[par[i][j - 1]][j - 1];
}
}
}
- dfs에서는 각 노드의 레벨을 d 배열에 저장하고, 조상노드의 정보를 저장할 배열의 0번째 칸에는 바로 위 부모의 정보를 저장해놓는다.
- 이후 f 함수에서는 조상의 정보를 갱신한다. 여기서 중요한 점화식이 나오는데
par[i][j] = par[par[i][j - 1]][j - 1];
→ 이게뭐지?! 갑자기 어디서 나온걸까.
자, 전처리했을 때의 상황을 살펴보자. 모든 노드는 자신의 레벨과 자신의 바로 위 부모를 알고 있다. 즉 par[node][0] 의 정보만 존재하는 상태이다.
우리가 필요한 것은 2^N 단위로 상위 부모를 알아내는 것이다.
위 그래프에서 예를들어 i = 12 j = 1 라고 가정하자.
par[12][2] = 12번 노드의 2^1위의 조상 즉, 12 보다 2칸위의 조상을 뜻한다. 그러므로 7이다. 그리고 7을 알고 있는 노드는 누가있을까 바로 내 바로위의 조상이 알고 있을 것이다. 당연하다. 할머니 할아버지는 당연히 엄마 아빠가 잘 알겠지.
그러므로 par[12][0] 을 호출한다. 그리고 나에게는 2칸위이지만, 엄마아빠에겐 1칸 위이다. 즉 j - 1번째 조상이다.
그래서 이것을 점화식으로 나타내면 par[i][j] = par[par[i][j - 1]][j - 1]; 공식이 나오는 것이다. 이것을 코드로 모두 나타내면 위와 같은 식이 된다.
LCA
대망의 LCA이다. 위에서 말했던 것 처럼 먼저 레벨을 맞춰주고 상위 조상을 살펴보는 코드를 만들어보자.
int lca(int x, int y) {
if (d[x] > d[y])
swap(x, y);
for (int i = 20; i >= 0; i--) {
if (d[y] - d[x] >= (1 << i))
y = par[y][i];
}
if (x == y)return x;
for (int i = 20; i >= 0; i--) {
if (par[x][i] != par[y][i]) {
x = par[x][i];
y = par[y][i];
}
}
return par[x][0];
}
먼저 위의 for문에서는 두 레벨의 차이를 비교하여 차이나는 칸 만큼 작은 노드를 올려준다.
if문을 해석해보면, x의 최고조상부터 아래로 내려오며 x의 깊이와 비교한다. 만약 x의 깊이가 2라고 할 때, d[par[x][i]] x의 2^i 번째 조상의 깊이가 3이라고 하면 x를 그 조상으로 갱신한다. 그리고 이번에는 3의 조상을 조사하다 보면 결국 x의 레벨과 같게 된다. 왜냐하면 레벨차가 1이면 i가 0일 때 같도록 갱신될 것이기 때문이다.
그런데 올려줬을 때 그것이 답일 수도 있으니 처리해주고
이제 두번째 for문을 돌리며 조상을 탐색한다. 그런데 이런 생각이 들 수 있다.
💡 2의 제곱으로 올라가면 그럼 3번째 위에 있는 조상이 정답이면 영원히 볼 수 가 없지않나?
나만 바보라서 이런생각을 한 것일수도 있지만 코드 보면 2^20번째 최고 조상부터 파악함을 알 수 있다. 그리고 “다르면” 노드가 갱신된다. 10, 12로 예를 들어보자 이 둘의 정답은 3칸 위인 3이 정답이다.
위 노드의 높이는 5밖에 안되기 때문에 점화식에 의해 이 이상의 값들 par[12][10] 값들은 모두 루트노드인 1일 것이다. 그러므로 20부터 시작하면 par[12][2] = 1, par[10][2] = 1 다음으로 par[12][1] = 6, par[1][1] = 7 일 때 달라졌으므로 x, y는 갱신된다 6과 7로.
그리고 6과 7은 i가 몇이던 간에 갱신될 일이 없다. 그러므로 끝이난다.
그리고 6,7의 바로 위 조상이 정답이 되는 것이다.
시간복잡도
dfs의 시간복잡도는 N개의 노드를 방문하므로 N
setNode의 시간복잡도는 DP를 갱신하므로 N * 20
그리고 LCA의 시간복잡도는 M*logN 이므로
총 TC = O(21 * N + M * logN)
만약 LCA2 문제라고 하면 N = 10만 M = 10만 이므로
210만 + 10만*6 = 270만이되어 1억을 넘지 않으므로 무난하게 통과 가능하다.
'CS > 자료구조,알고리즘' 카테고리의 다른 글
| 벨만-포드 알고리즘 (Bellman-Ford Algorithm) (0) | 2024.01.15 |
|---|---|
| 플로이드-워셜 알고리즘 (2) | 2023.12.26 |
| 이분 탐색의 이해 (0) | 2023.07.02 |
| 문자열 관리 자료구조 - 트라이(Trie) 개념/구현 (0) | 2023.02.24 |
| DFS를 활용한 순열 (0) | 2023.02.23 |


